意大利数学家 Leonardo Fibonacci(1170-1250)被许多人认为是中世纪最有才华的人。他普及了许多以他命名的数列,作为兔子逐代繁殖的模型。但后来,人们发现这些数字可以用于许多其他情况,其中包括外汇交易。
一点数学知识
该数列从数字 0 和 1 开始,然后是两者之和:组合在一起后,数列的起始数字是 0,1,1,2,3,5,8,13,21 等。
数学极限
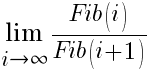
或者简而言之,斐波那契数列中任意大数与后一位数的比值为 0.618,而极限

或者一个斐波那契数字除以它后面第二个数的比率为 0.382。减去这两个数字得到 0.236,其平均值为 0.500,其和为 1.000。最后,1.000 − 0.236 = 0.764。
斐波那契应用于外汇中:回调位和扩展位
我们刚刚学到的数字——0,0.236,0.382,0.500,0.618,0.764 和 1.000——被称为斐波那契回调位。通过类似于上一章节中的计算方式,我们可以得出以下比率:0,0.382,0.618,1.000,1.382 和 1.618。这些比率被称为斐波那契扩展位。
一旦您发现最高点(HH)之后迅速出现最低点(LL),并使用它们作为极值来绘制交易平台上的斐波那契回调位或扩展位,则这些比率代表着相对于 HH/LL 范围的回调位或扩展位;在该范围内,货币对更容易出现支撑位或阻力位,即货币对将出现逆转走势的价位。
高级技巧:斐波那契扇形和其他技巧
除了回调位和扩展位以外,这些比率在货币交易中还有其他应用:实际上,还有许多其他工具建立在这些比率的基础之上。我们没有时间详细地介绍所有内容,但还有一种常用的工具值得提到:斐波那契扇形。它使用上述比率绘制支撑/阻力线,但是将趋势线合并为一个点(即“扇形”)。
斐波那契为什么可靠
据推测,斐波那契比率在交易中非常有用,这是因为它们得到了众多交易者的广泛使用并且进一步影响了市场和交易者,而不是因为斐波那契比率的自身原因。
虽然这一问题还没有得到确切的答案,但值得指出的是,要影响一个每天涉及数万亿美元交易的市场可不是一件容易办到 的事。
无论如何,即使您首先难以掌握这些工具的使用方式,但这些工具一定会提升您的交易体验。